【統計】ロジスティック回帰分析

ロジスティック回帰分析について。

【目次】

計算式等
ノート
プログラムコード
交差エントロピー誤差の偏微分
参考

今回はモデル作成まで。モデルの評価は別記事で。

計算式等

ロジスティック回帰は二値分類（ $y\in\{0,1\}$ ）で用いられる分析手法。
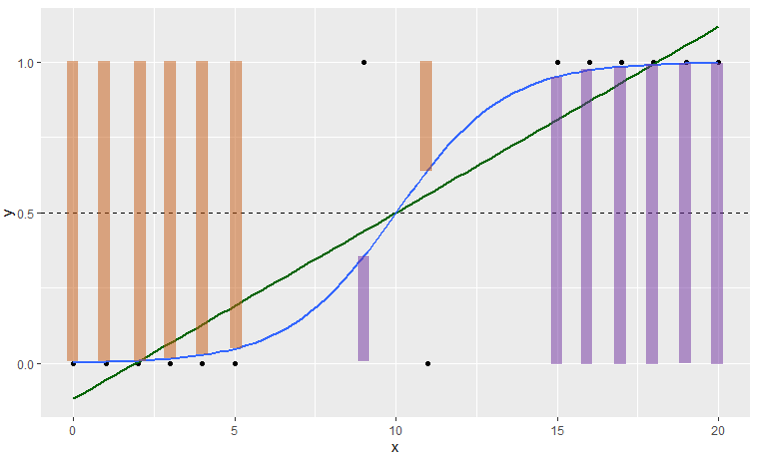
モデル式は回帰分析と似ているが、シグモイド関数を使って０～１の範囲の結果を出すことが特徴（通常の回帰分析では０～１の範囲を超えてしまい、解釈不能な結果になってしまう）。
（青線：ロジスティック回帰、緑線：単回帰分析）

f:id:cochineal19:20210112220847p:plain

モデル式、シグモイド関数および損失関数はそれぞれ次のとおり。

モデル式
$\quad \widehat{y}=\beta _{0} + \beta _{1} x_{1} +...+ \beta _{k} x_{k} = \beta ^{T} X$

シグモイド関数（活性化関数）
$\quad z=\sigma \left( \widehat{y} \right) = \dfrac{1}{1+exp \left( -\widehat{y} \right)} = \left( 1 + exp \left( -\widehat{y} \right)\right)^{-1} = \dfrac{exp \left( \widehat{y} \right)}{1 + exp \left(\widehat{y}\right)}$

交差エントロピー誤差（分類問題の損失関数）
$\quad E\left(\beta\right)=-\sum \{ y_{i} \cdot ln\left(z_{i}\right) + \left(1-y_{i} \right) \cdot ln \left( 1-z_{i} \right) \} =0$
　※ ln( ) は自然対数。 $y_{i}$ は実測値で $y_{i}\in\{0,1\}$ です（正解ラベルとも言われます）。

交差エントロピー誤差は、対数尤度にマイナスをつけて０を最小値としたもの（負の対数尤度）。式の第一項（ $y_{i} \cdot ln\left(z_{i}\right)$ ）で実際にイベントが起きたデータ（ $y_{i}=1$ ）に対する予測誤差を計算する（予測90%なら10%が誤差）。式の第二項（ $\left(1-y_{i} \right) \cdot ln \left( 1-z_{i} \right)$ ）でイベントが起きなかったデータ（ $y_{i}=0$ ）に対する予測誤差を計算する（予測10%なら10%が誤差）。
第一項も第二項も $y_{i}=z_{i}$ の時に $ln\left(1\right)=0$ となることから、実測値と予測値が完全一致すれば合計０で誤差なしとなる。
※イメージ的には紫の棒が $y_{i}=1$ の時の $z_{i}$ 、オレンジの棒が $y_{i}=0$ の時の $1-z_{i}$ 。

f:id:cochineal19:20210112230833p:plain

対数尤度関数の計算方法についても掲載。
対数尤度関数
$\quad ln\ L\left( \beta\right)=f \left(y_{i}, z_{i}\right)=\sum \{ y_{i} \cdot ln\left(z_{i}\right) + \left(1-y_{i} \right) \cdot ln \left( 1-z_{i} \right) \}$
尤度関数
$\quad L \left( \beta \right) =\Pi \{ z_{i}^{y_{i}} \times \left( 1-z_{i} \right)^{ \left( 1 - y_{i} \right) } \}$

※尤度関数は０～１の確率を "かけ算" するため、値がかなり小さくなってしまう（コンピュータ計算に不向き）。そのため、対数変換して確率の "足し算" とした対数尤度関数が広く使われる。

そして、肝心の回帰係数 β の計算方法は次のとおり。
回帰係数 β の計算方法

$\quad \dfrac{\partial E\left( \beta \right) }{\partial \beta }=\dfrac{\partial E\left( \beta\right) }{\partial z}\dfrac{\partial z}{\partial \widehat{y}}\dfrac{\partial \widehat{y}}{\partial \beta }=\sum \left( z_{i}-y_{i}\right) x_{i}=0$

式中に $z_{i}$ があるため、"回帰係数 β を算出するために回帰係数 β が必要" ということになる。本記事ではニュートン・ラフソン法（以降、ニュートン法）による回帰係数の更新方法を取り上げる。

ニュートン法
$\quad \beta ^{new}=\beta^{old} - H^{-1}\nabla E\left(\beta \right)$

ニュートン法では既存の回帰係数 $\beta ^{old}$ と演算後の回帰係数 $\beta ^{new}$ との差がなくなるまで更新を繰り返す。最適解の算出には交差エントロピー誤差のヘッセ行列（H）と重み付き行列（R）を用いる。このRはシグモイド関数の微分の対角行列。
$\quad \nabla E \left( \beta \right) = \sum \left( z_{i} - y_{i} \right) x_{i} = \left( Z - Y \right) X^{T} = \sum x_{i} y_{i} - \sum x_{i} z_{i}$
$\quad H=\nabla\nabla E \left( \beta \right)=\sum z_{i}\left(1-z_{i}\right)x_{i}x_{i}^{T}=X^{T}RX$
$\quad R = z_{i} \left( 1 - z_{i} \right) = \dfrac{1}{1+exp \left( -y \right)} \times \dfrac{exp \left( -y \right) }{1+exp \left( -y \right)} = \dfrac{ exp \left( -y \right)}{\left( 1+exp \left( -y \right)\right)^{2}}$

これらをまとめると次の図解。
f:id:cochineal19:20210117010158p:plain

近似的な方法

簡易的にロジスティック回帰分析を行う方法として、ロジット変換した値を目的変数にした回帰分析がある。二値を Yes / No の数で表すとロジット変換は次の式。
$\quad logit = ln\left( \dfrac{P_{yes}}{1-P_{yes}}\right) = ln\left( \dfrac{N_{yes}/N_{all}}{N_{no}/N_{all}}\right) = ln\left( \dfrac{N_{yes}}{N_{no}}\right)$

なお、０の対数変換 $ln(0)$ は計算できないため、0.5 を加算してロジット変換する方法がある。これを経験ロジットと言う。
$\quad 経験logit = ln\left( \dfrac{N_{yes}+0.5}{N_{no}+0.5}\right)$

また、この回帰分析に重みを加えたい場合、ロジットの分散の逆数を重みとする（重み付き回帰分析）。経験ロジットを使う場合は３つ目の式。
$\quad w_{i}=p_{i}\left( 1-p_{i}\right) n_{i}$
$\qquad p_{i}=\dfrac{N_{yes}}{N_{all}}$
$\qquad p_{i}=\dfrac{\left(N_{yes}+0.5 \right)}{\left(N_{all}+1\right)}$

最後に、覚えておくと良さそうなシグモイド関数の性質をメモ。

シグモイド関数の性質
$\quad z=\dfrac{1}{1+exp\left(-\widehat{y}\right)}$
$\quad 1-z=\dfrac{exp\left(-\widehat{y}\right)}{1+exp\left(-\widehat{y}\right)}$
$\quad \dfrac{z}{1-z}=exp\left(-\widehat{y}\right)$ 　←オッズ比

ノート

今回も簡単なデータで計算手順を見てみる。

■ サンプルデータ

X₁	X₂	N_yes	N_all	P_yes	Logit	経験Logit
5	0	1	20	0.050	-2.944	-2.565
5	1	6	22	0.273	-0.981	-0.932
10	0	9	25	0.360	-0.575	-0.552
10	1	16	30	0.533	0.134	0.129
15	0	19	30	0.633	0.547	0.528
15	1	28	30	0.933	2.639	2.434

今回は近似的な方法で算出した回帰係数 β を初期値にする
その後、ニュートン法を用いて回帰係数 β を更新し、最適解を探す。

初期値設定

f:id:cochineal19:20210130204334p:plain

LINEST関数で計算。目的変数は経験ロジット。今回は重み付き回帰分析はしていない（単に初期値を得るためなので）。
回帰係数 β はそれぞれ $\beta_{0}=-4.09208,\ \beta_{1}=0.32291,\ \beta_{2}=1.40674$ 。
※LINEST関数の使い方は単回帰分析で記載。

cochineal19.hatenablog.com

回帰係数 β の更新１回目

f:id:cochineal19:20210130205729p:plain

初期値の回帰係数 β をもとに予測値 $\widehat{y},\ z$ を算出する。
サンプルデータの１行目は $x_{1}=5,\ x_{2}=0$ なので次のとおり。※上図Excel A列の $x_{0}$ は切片項用に 1 を設定。
$\quad \widehat{y}=-4.09208+0.32291\times5+1.40674\times0\fallingdotseq-2.478$
$\quad z=\dfrac{1}{1+exp\left(-\widehat{y}\right)}=\dfrac{1}{exp\left(-1\times-2.478\right)}\fallingdotseq 0.077$

次にヘッセ行列を求める。
＜式の再掲＞
$\quad H=\nabla\nabla E \left( \beta \right)=\sum z_{i}\left(1-z_{i}\right)x_{i}x_{i}^{T}=X^{T}RX$
$\quad R = z_{i} \left( 1 - z_{i} \right) = \dfrac{1}{1+exp \left( -\widehat{y} \right)} \times \dfrac{exp \left( -\widehat{y} \right) }{1+exp \left( -\widehat{y} \right)} = \dfrac{ exp \left( -\widehat{y} \right)}{\left( 1+exp \left( -\widehat{y} \right)\right)^{2}}$

サンプルデータの１行目を取り上げると R は $R=z_{1}\left(1-z_{1}\right)=0.077\left(1-0.077\right)\fallingdotseq 0.071$ 。
ヘッセ行列は次のとおりで、今回は切片＋説明変数２つの３次元なので３×３の行列になる。

$\quad H=\begin{bmatrix} \sum H_{00} \quad \sum H_{01} \quad \sum H_{02} \\ \sum H_{10} \quad \sum H_{11} \quad \sum H_{12} \\ \sum H_{20} \quad \sum H_{21} \quad \sum H_{22} \end{bmatrix}=\begin{bmatrix} -27.1181 \quad -289.7161 \quad -13.9390 \\ -289.7161 \quad -3455.7462 \quad -132.4044 \\ -13.9390 \quad -132.4044 \quad -13.9390 \end{bmatrix}$

$\qquad \sum H_{00}=\sum x_{0i}\times x_{0i}\times R_{i}\times N_{all\ i},\quad \sum H_{01}=\sum x_{0i}\times x_{1i}\times R_{i}\times N_{all\ i}, \quad \sum H_{02}=\sum x_{0i}\times x_{2i}\times R_{i}\times N_{all\ i}$
$\qquad \sum H_{10}=\sum x_{1i}\times x_{0i}\times R_{i}\times N_{all\ i},\quad \sum H_{11}=\sum x_{1i}\times x_{1i}\times R_{i}\times N_{all\ i},\quad \sum H_{12}=\sum x_{1i}\times x_{2i}\times R_{i}\times N_{all\ i}$
$\qquad \sum H_{20}=\sum x_{2i}\times x_{0i}\times R_{i}\times N_{all\ i},\quad \sum H_{21}=\sum x_{2i}\times x_{1i}\times R_{i}\times N_{all\ i},\quad \sum H_{22}=\sum x_{2i}\times x_{2i}\times R_{i}\times N_{all\ i}$

※ 今回の集計表はレコードをまとめているため、計算式に「 $\times N_{all\ i}$ 」を入れている。

さらに $\nabla E \left( \beta \right)$ を求める。

$\quad \nabla E \left( \beta \right) = \sum \left( z_{i} - y_{i} \right) x_{i} = \left( Z - Y \right) X^{T} = \sum x_{i} y_{i} - \sum x_{i} z_{i}$
$\quad \nabla E \left( \beta \right) = \begin{bmatrix} \sum \left( x_{0i} \times N_{yes \ i} \right) - \sum \left( x_{0i} \times z_{i} \times N_{all \ i} \right) \\ \sum \left( x_{1i} \times N_{yes \ i} \right) - \sum \left( x_{1i} \times z_{i} \times N_{all \ i} \right) \\ \sum \left( x_{2i} \times N_{yes \ i} \right) - \sum \left( x_{2i} \times z_{i} \times N_{all \ i} \right) \end{bmatrix}=\begin{bmatrix} 79 - 80.84 \\ 990 - 1008.99 \\ 50 - 51.49 \end{bmatrix} = \begin{bmatrix} -1.842 \\ -18.990 \\ -1.489 \end{bmatrix}$

※ 今回の集計表はレコードをまとめているため、計算式に「 $\times N_{all\ i}$ 」と「 $\times N_{yes\ i}$ 」を入れている。「 $\sum x_{i} y_{i}$ 」は $y=1$ の時だけ０以外の値を持つため「 $\times N_{yes\ i}$ 」としている。

これら計算結果から回帰係数 β を更新すると次のようになる。
$\quad \beta ^{new}=\beta^{old} - H^{-1}\nabla E\left(\beta \right)$
$\quad \beta ^{new}=\begin{bmatrix} -4.09208 \\ 0.32291 \\ 1.40674 \end{bmatrix} - \begin{bmatrix} -27.1181 \quad -289.7161 \quad -13.9390 \\ -289.7161 \quad -3455.7462 \quad -132.4044 \\ -13.9390 \quad -132.4044 \quad -13.9390 \end{bmatrix}^{-1}\begin{bmatrix} -1.842 \\ -18.990 \\ -1.489 \end{bmatrix}=\begin{bmatrix} -4.09514 \\ 0.32093 \\ 1.32180 \end{bmatrix}$

$\beta_{0}=-4.09514,\ \beta_{1}=0.32093,\ \beta_{2}=1.32180$ それぞれの更新前後の差は 0.00306, 0.00198, 0.08494 で差があるので更新を続ける。

回帰係数 β の更新２回目

f:id:cochineal19:20210130211424p:plain

更新２回目は $\beta_{0}=-4.10022,\ \beta_{1}=0.32135,\ \beta_{2}=1.32386$ で更新前後の差は 0.00508, -0.00043, -0.00206 。だいぶ良くなったが、まだ差があるので更新する。

回帰係数 β の更新３回目

f:id:cochineal19:20210130211714p:plain 更新３回目は $\beta_{0}=-4.10022,\ \beta_{1}=0.32135,\ \beta_{2}=1.32386$ で更新前後の差は 0.000000, 0.000000, 0.000000 。更新前後の回帰係数 β が同値で差がなくなった。

よって更新はここまでにして次を最終モデルとする。

$\quad \widehat{y}=-4.10022 + 0.32135 x_{1} + 1.32386 x_{2}$

Rでの実行：

> ads <- data.frame(
+   x1=c(rep(5,20),rep(5,22),rep(10,25),rep(10,30),rep(15,30),rep(15,30))
+   ,x2=c(rep(0,20),rep(1,22),rep(0,25),rep(1,30),rep(0,30),rep(1,30))
+   ,y=c(rep(0,19),rep(1,1),rep(0,16),rep(1,6),rep(0,16),rep(1,9),rep(0,14),rep(1,16),rep(0,11),rep(1,19),rep(0,2),rep(1,28))
+ )
> fit1 <- glm(y ~ x1 + x2, family=binomial, data=ads)
> summary(fit1)
Call:
glm(formula = y ~ x1 + x2, family = binomial, data = ads)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.0812  -0.8307   0.4935   0.8906   2.2684  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -4.10022    0.72055  -5.690 1.27e-08 ***
x1           0.32135    0.05562   5.778 7.58e-09 ***
x2           1.32386    0.40344   3.281  0.00103 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)
    Null deviance: 217.64  on 156  degrees of freedom
Residual deviance: 164.56  on 154  degrees of freedom
AIC: 170.56
Number of Fisher Scoring iterations: 4

SASでの実行：

data ads(drop=i);
  do i=1 to  1; x1= 5; x2=0; y=1; output; end;
  do i=1 to 19; x1= 5; x2=0; y=0; output; end;
  do i=1 to  6; x1= 5; x2=1; y=1; output; end;
  do i=1 to 16; x1= 5; x2=1; y=0; output; end;
  do i=1 to  9; x1=10; x2=0; y=1; output; end;
  do i=1 to 16; x1=10; x2=0; y=0; output; end;
  do i=1 to 16; x1=10; x2=1; y=1; output; end;
  do i=1 to 14; x1=10; x2=1; y=0; output; end;
  do i=1 to 19; x1=15; x2=0; y=1; output; end;
  do i=1 to 11; x1=15; x2=0; y=0; output; end;
  do i=1 to 28; x1=15; x2=1; y=1; output; end;
  do i=1 to  2; x1=15; x2=1; y=0; output; end;
run;

ods output LackFitChiSq=HOSLEM1;
proc logistic data=ads descending;
  model y(event='1') = x1 x2 / outroc=ROC1 lackfit;
  output out=OutDS;
run;

f:id:cochineal19:20210130212212p:plain

統計ソフトってすごく便利。。と体感した。

プログラムコード

■ Rのコード

fit <- glm(y ~ x1 + x2, family=binomial, data=ads)
summary(fit)

■ SASのコード

proc logistic data=[InputDS] descending;
  model y(event='1') = x1 x2;
  output out = [OutDS];
run; quit;

■ Pythonのコード

整備中

交差エントロピー誤差の偏微分

回帰係数 β の計算方法で示した交差エントロピー誤差の偏微分の詳細。
「連鎖律」という方法で微分する。

交差エントロピー誤差
$\quad E\left(\beta\right)=-\sum \{ y_{i} \cdot ln\left(z_{i}\right) + \left(1-y_{i} \right) \cdot ln \left( 1-z_{i} \right) \} =0$
偏微分
$\quad \dfrac{\partial E\left( \beta \right) }{\partial \beta }=\dfrac{\partial E\left( \beta\right) }{\partial z}\dfrac{\partial z}{\partial \widehat{y}}\dfrac{\partial \widehat{y}}{\partial \beta }$
$\qquad \qquad =-\sum \{ y_{i} \times \dfrac{1}{z_{i}} \times z_{i}\left( 1-z_{i}\right) \times x_{i} + \left(1-y_{i}\right) \times \dfrac{1}{1-z_{i}} \times \left( -z_{i}\left( 1-z_{i} \right) \right) \times x_{i} \}$
$\qquad \qquad =-\sum \{ y_{i} \left( 1-z_{i}\right) + \left(1-y_{i}\right) \left( -z_{i} \right)\} x_{i}$
$\qquad \qquad =-\sum \{ y_{i} - y_{i} z_{i} - z_{i} + y_{i} z_{i}\} x_{i}$
$\qquad \qquad =-\sum \{ y_{i} - z_{i} \} x_{i}$
$\qquad \qquad =\sum \left( z_{i}-y_{i}\right) x_{i}=0$

図解するとこんな感じ。シグモイド関数の微分は公式で z(1-z) になる。

f:id:cochineal19:20210117223042p:plain

-----

なお、SASやRのロジスティック回帰では「ニュートン法」ではなく、「フィッシャースコアリング法」が用いられているようだった（記事を書き終わってから気づいた）。
この方法は、ニュートン法で使った「ヘッセ行列」を「フィッシャー情報行列」に置き換えたもの。計算コストが良い様子。
今回は更新の仕組みが分かれば良いと思っていたため、この記事は終了。

フィッシャースコアリング法について Wikipedia を参照。

尤度方程式 - Wikipedia