【機械学習_Python】Ridge回帰、Lasso回帰、Elastic Net回帰

Ridge回帰、Lasso回帰、Elastic Net回帰についてのメモ。
本記事は「機械学習」における回帰分析という視点が強め。

Ridge回帰等と区別するため、最小二乗法による一般的な回帰分析を最小二乗回帰分析（ordinary least square：OLS）と呼ぶ。

本記事では Python の sklearn を用い、損失関数の計算式は scikit-learn 0.24.2 の仕様のものを記載している。

【目次】

はじめに① ～最小二乗回帰分析（ordinary least square：OLS）のおさらい～
はじめに② ～正則化法の導入～
Ridge回帰
Lasso回帰（Least absolute shrinkage and selection operator regression）
Elastic Net回帰
bostonデータで各モデルを実行してみる
参考

はじめに① ～最小二乗回帰分析（ordinary least square：OLS）のおさらい～

最小二乗回帰分析については次の記事も参照。統計学寄りで書いた記事。
・【統計】単回帰分析 - こちにぃるの日記
・【統計】重回帰分析 - こちにぃるの日記

回帰モデル、予測式及び回帰係数（重み）は次のとおり（上の記事より抜粋）。

$\quad y=\beta_{0}+\beta_{1}x_{1}+\beta_{2}x_{2}+...+\beta_{k}x_{k} + \varepsilon\ ,\quad\sim\varepsilon: N\left(0,\sigma^{2}\right)$

$\quad \widehat{y}_{i}=b_{0}+b_{1}x_{1i}+b_{2}x_{2i}+...+b_{k}x_{ki}$

$\quad b_{0}=\overline{y} - \left( b_{1}\overline{x_{1}}+b_{2}\overline{x_{2}}+...+b_{k}\overline{x_{k}} \right)$

$\quad \begin{bmatrix} b_{1} \\ b_{2} \\ \ \vdots \\ b_{k} \end{bmatrix} = \begin{bmatrix} S_{x_{1}x_{1}} \quad S_{x_{1}x_{2}} \quad \ldots \quad S_{x_{1}x_{k}} \\ S_{x_{2}x_{1}} \quad S_{x_{2}x_{2}} \quad \ldots \quad S_{x_{2}x_{k}} \\ \ \vdots \qquad \ \vdots \qquad \ \ddots \qquad \ \vdots \\ S_{x_{k}x_{1}} \quad S_{x_{k}x_{2}} \quad \ldots \quad S_{x_{k}x_{k}} \end{bmatrix}^{-1} \begin{bmatrix} S_{x_{1}y} \\ S_{x_{2}y} \\ \ \vdots \\ S_{x_{k}y} \\ \end{bmatrix}$

これを行列表現すると回帰係数（重み）は次のように求められる。

正規方程式

$\quad \left( \boldsymbol{X}^{t}\boldsymbol{X}\right) \widehat{\boldsymbol{\beta }}=\boldsymbol{X}^{t}\boldsymbol{Y}$

$\quad \widehat{\boldsymbol{\beta} }=\left( \boldsymbol{X}^{t} \boldsymbol{X} \right) ^{-1}\left( \boldsymbol{X}^{t} \boldsymbol{Y} \right)$

　　※ ^ t = 転置、^ -1 = 逆行列

Pythonコード

#-- インポート
from sklearn.linear_model import LinearRegression
from sklearn import metrics
import numpy as np
  
#-- 訓練・テスト
mod1 = LinearRegression()
mod1.fit(X_train, y_train)  #-- 訓練データで学習
y_pred1 = mod1.predict(X_test)  #-- テストデータで予測
  
#-- モデル評価
R2sq = mod1.score(X_test, y_test)  #-- 決定係数（寄与率）の算出
MAE  = metrics.mean_absolute_error(y_test, y_pred1)  #--  MAEの算出
RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred1)) #-- RMSEの算出
  
#-- 切片、回帰係数（重み）の取得
print("切片 = ", mod1.intercept_)
print("回帰係数 = ", mod1.coef_)

はじめに② ～正則化法の導入～

最小二乗回帰分析では、損失関数 $L$ を実測値と予測値の差（残差 $e_{i} = y_{i} - \hat{y_{i}}$ ）とし、当該関数の最小化を目的とした。

$\quad L = || \boldsymbol{y} - \boldsymbol{X \beta} || _{2}^{2} = {\displaystyle \Sigma_{i=1}^{n}}\left(y_{i} - \hat{y_{i}}\right)^{2} = {\displaystyle \Sigma_{i=1}^{n}} e_{i}^{2}$

最小二乗回帰分析は機械学習の分野でも「教師あり学習」として広く用いられる手法であるが、複数の特徴量（説明変数）を扱うモデルにおいては次の問題に注意が必要となる。特に「過学習」は将来の予測に重きを置く機械学習の分野で良く耳にするワードである。

・多重共線性（Multicollinearity）
・過学習（Over fitting）

これら問題への対策の１つとして正則化法がある。
式としては、最小二乗回帰分析の損失関数 $L$ に正則化項 $\lambda \left( Lp \right)$ （ペナルティ項、罰則項）を加えたものを目的関数とする。

$\quad L = || \boldsymbol{y} - \boldsymbol{X \beta} || _{2}^{2} + \lambda \left( Lp \right)= {\displaystyle\Sigma_{i=1}^{n}}\left(y_{i} - \hat{y_{i}}\right)^{2} + \lambda \left( Lp \right)$

正則化項のラムダ $\lambda$ はハイパーパラメータであり、ラムダ $\lambda$ を０にすれば通常の最小二乗回帰分析となる。
また、 $Lp$ は回帰係数（重み）を用いたLpノルムであり、L1またはL2ノルムが用いられる。損失関数（残差）を小さくするために特徴量（説明変数）を多くすれば、Lpノルムが大きくなり罰則として働く。

L1ノルム（マンハッタン距離）

$\quad L_{1} = ||\boldsymbol{\beta}||_{1} = {\displaystyle\Sigma_{j=1}^{m}} |\beta_{j}|$

L2ノルム（ユーグリッド距離）

$\quad L_{2} = ||\boldsymbol{\beta}||_{2} = \sqrt{ {\displaystyle \Sigma_{j=1}^{m}} \beta_{j}^{2}}$

回帰係数２つのL1ノルムとL2ノルムの2乗は次のとおりである。
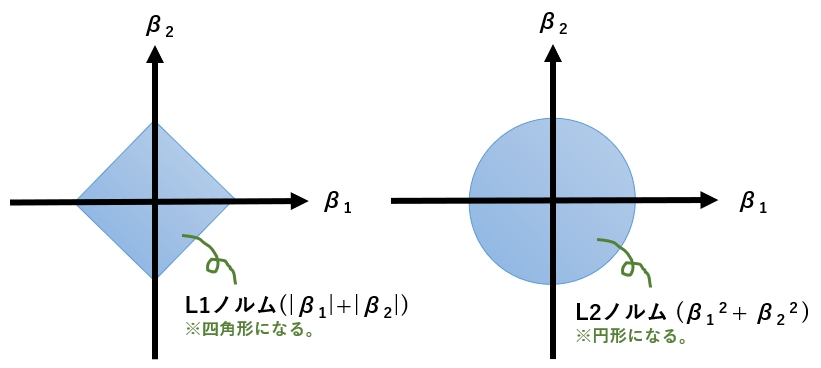
f:id:cochineal19:20210516132056p:plain:w500

なお、Lp正則化を行う場合、特徴量（説明変数）を事前に標準化しておく必要がある。

Pythonコード

from sklearn.preprocessing import StandardScaler
 
SS = StandardScaler()
X_train_SS = SS.fit_transform(X_train)
X_test_SS  = SS.transform(X_test)

Ridge回帰

Ridge回帰はL2正則化を用いた方法である。L2ノルム（ユーグリッド距離）の２乗を用いる。

$\quad L = || \boldsymbol{y} - \boldsymbol{X \beta} || _{2}^{2}+\lambda || \boldsymbol{\beta} || _{2}^{2} = {\displaystyle\Sigma_{i=1}^{n}}\left(y_{i} - \hat{y_{i}}\right)^{2} +\lambda {\displaystyle\Sigma_{j=1}^{m}} \beta_{j}^{2}$

Ridge回帰の特徴は、多重共線性の問題を回避できるところである。
最小二乗回帰分析のセクションで正規方程式を示したが、最小二乗回帰分析では逆行列 $\left( X^{t}X\right) ^{-1}$ が存在しない場合、多重共線性の問題が生じる。

$\quad \widehat{\boldsymbol{\beta} }=\left( \boldsymbol{X}^{t} \boldsymbol{X} \right) ^{-1}\left( \boldsymbol{X}^{t} \boldsymbol{Y} \right) \quad \verb|（再掲）|$

Ridge回帰では、正規方程式に $\lambda \boldsymbol{ I }$ が加わることで逆行列が計算できるようになり、多重共線性の問題が解消される。なお、 $\boldsymbol{ I }$ は単位行列、 $\lambda$ はスカラーでハイパーパラメータである。

$\quad \widehat{\boldsymbol{\beta} }=\left( \boldsymbol{X}^{t} \boldsymbol{X} + \lambda \boldsymbol{I}\right) ^{-1}\left( \boldsymbol{X}^{t} \boldsymbol{Y}\right)$

Ridge回帰では特徴量選択（変数選択）こそ出来ないが、相関の高いデータセットに対して安定性があり、汎化性の向上が見込める。

Pythonコード

from sklearn.linear_model import Ridge
mod1 = Ridge(alpha=1)
mod1.fit(X_train_SS, y_train_SS)
 
#-- 以降の使い方はLinearRegressionと同じなので割愛

※引数 alpha が本記事内のハイパーパラメータ：λ（ラムダ）にあたる。コード例の設定値はデフォルト。デフォルトのままで良いなら記載不要。

Lasso回帰（Least absolute shrinkage and selection operator regression）

Lasso回帰はL1正則化を用いた方法である。L1ノルム（マンハッタン距離）を用いる。

$\quad L = \dfrac{1}{2n} || \boldsymbol{y} - \boldsymbol{X \beta} || _{2}^{2}+\lambda || \boldsymbol{\beta} || _{1} = \dfrac{1}{2n}{\displaystyle\Sigma_{i=1}^{n}}\left(y_{i} - \hat{y_{i}}\right)^{2} +\lambda {\displaystyle\Sigma_{j=1}^{m}} | \beta_{j} |$

Lasso回帰の特徴は、いくつかの回帰係数（重み）が０になることであり、この性質から特徴量選択（変数選択）を自動的に行うことができる。スパース推定と言われる。

Lasso回帰による特徴量選択（変数選択）は非常に有用であるが、使用の際は次の性質に注意されたい。

サンプルサイズn以上の特徴量を選択できない。
相関の高い特徴量同士では片方が選択されない可能性がある。重要な特徴量同士の相関が高い場合、特に注意。
特徴量間の相関が高いデータセットでは、少しの変動で選択される特徴量が変わる不安定さがあるようである。

回帰係数（重み）の計算方法は現時点で理解できていないため割愛する。
PythonのskleanやRのglmnetではCoordinate Descent法（CD法、座標降下法）が用いられているようである。

次の図は、正則化の概念を示した良く見かける図であり、損失関数（最小二乗誤差）の最適値と制約条件内（水色の円形と四角形）での最適値を示したものである。

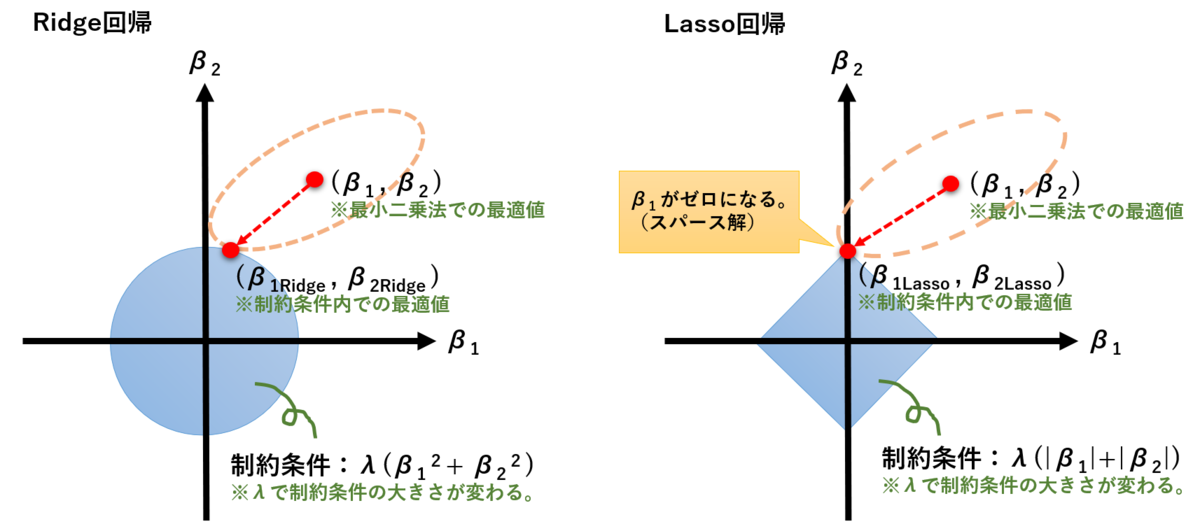
f:id:cochineal19:20210516134227p:plain:w700

制約条件内の最適値が線上にあれば回帰係数（重み）が０になるため特徴量選択ができる。
この制約条件（水色の円形と四角形）の大きさはハイパーパラメータ：λ（ラムダ）で調整できる。

Pythonコード

from sklearn.linear_model import Lasso
mod1 = Lasso(alpha=1)
mod1.fit(X_train_SS, y_train_SS)
  
#-- 以降の使い方はLinearRegressionと同じなので割愛

※引数 alpha が本記事内のハイパーパラメータ：λ（ラムダ）にあたる。コード例の設定値はデフォルト。デフォルトのままで良いなら記載不要。

Elastic Net回帰

Elastic Net回帰はL1正則化とL2正則化の両方を用いた方法である。

$\quad \rho = L_{1}Ratio \qquad *\ \rho=[ 0,\ 1]$

$\quad L = \dfrac{1}{2} || \boldsymbol{y} - \boldsymbol{X \beta} || _{2}^{2}+\lambda \ \rho \ || \boldsymbol{\beta }|| _{1} + \dfrac{\lambda \left(1 - \rho \right)}{2} || \boldsymbol{\beta} || _{2}^{2}$

$\qquad = \dfrac{1}{2} {\displaystyle\Sigma_{i=1}^{n}}\left(y_{i} - \hat{y_{i}}\right)^{2} +\lambda \ \rho \ {\displaystyle\Sigma_{j=1}^{m}} | \beta_{j}| + \dfrac{\lambda \left(1 - \rho \right)}{2} {\displaystyle\Sigma_{j=1}^{m}} \beta_{j}^{2}$

L1正則化の「特徴量選択」とL2正則化の「特徴量間の相関の高いデータセットに対する安定性」を組み合わせた方法であり、L1正則化とL2正則化の比率（L1-Ratio）を指定することでモデルの調整ができる。L1-Ratioはハイパーパラメータである。

Ridge回帰やLasso回帰に比べて、Elastic Net回帰が必ずしも良いという訳ではなく、最終的には決定係数やRMSE等の評価指標を用いて最良モデルを選択する。

Elastic Net回帰は式の通り、L1-Ratio=1でLasso回帰と同等となるが、L1-Ratio=0の時はRidge回帰とイコールにならない。
※ただし、Rのglmnetライブラリでは、Elastic Netの式をベースとしてL1-Ratio=1をLasso回帰、L1-Ratio=0をRidge回帰としているようである。
https://cran.r-project.org/web/packages/glmnet/glmnet.pdf
https://cran.r-project.org/web/packages/glmnet/vignettes/glmnet.pdf

Pythonコード

from sklearn.linear_model import ElasticNet
mod1 = ElasticNet(alpha=1, l1_ratio=0.5)
mod1.fit(X_train_SS, y_train_SS)
  
#-- 以降の使い方はLinearRegressionと同じなので割愛

※引数 alphaとl1_ratio が本記事内のハイパーパラメータ：λ（ラムダ）とρ（ロー、L1-ratio）にあたる。コード例の設定値はデフォルト。デフォルトのままで良いなら記載不要。

bostonデータで各モデルを実行してみる

bostonデータを使って最小二乗回帰、Ridge回帰、Lasso回帰、Elastic Net回帰を実行してみる。

from sklearn.linear_model import LinearRegression, Ridge, Lasso, ElasticNet
from sklearn import datasets, model_selection, preprocessing, metrics
import pandas as pd
import numpy as np

#-- ロード
ROW = datasets.load_boston()
ADS = pd.DataFrame(ROW.data, columns=ROW.feature_names).assign(target=np.array(ROW.target))

#-- 分割
X_train, X_test, y_train, y_test = model_selection.train_test_split(
        ADS[ROW.feature_names], ADS["target"], test_size=0.3, random_state=1)

#-- 標準化
SS = preprocessing.StandardScaler()
X_train_SS = SS.fit_transform(X_train)
X_test_SS  = SS.transform(X_test)

#-- 回帰分析
lm1 = {"最小二乗回帰":LinearRegression()
       ,"Lasso回帰":Lasso(alpha=1)
       ,"Ridge回帰":Ridge(alpha=1)
       ,"ElasticNet回帰 L1-Ratio=0"  :ElasticNet(alpha=1, l1_ratio=0)
       ,"ElasticNet回帰 L1-Ratio=0.5":ElasticNet(alpha=1, l1_ratio=0.5)
       ,"ElasticNet回帰 L1-Ratio=1"  :ElasticNet(alpha=1, l1_ratio=1)
       }

tmp1 = pd.DataFrame(["決定係数","MAE","RMSE"], columns=["評価指標"])
tmp2 = pd.DataFrame(ROW.feature_names, columns=["特徴量"])

for modnm, modcd in lm1.items(): 
    mod1 = modcd
    mod1.fit(X_train_SS, y_train)
    y_pred1 = mod1.predict(X_test_SS)
    R2sq = mod1.score(X_test_SS, y_test)
    MAE  = metrics.mean_absolute_error(y_test, y_pred1)
    RMSE = np.sqrt(metrics.mean_squared_error(y_test, y_pred1))
    tmp1[modnm] = [R2sq, MAE, RMSE]
    tmp2[modnm] = mod1.coef_