ARIMA、SARIMA、SARIMAXモデルをRで試してみる。
【目次】
用意したデータ
今回、横浜市の月別火災発生件数を例として扱う。
ソースは横浜市のオープンデータより取得。
このデータは2000年1月~2019年12月の20年間240カ月分ある。
更に火災と関連がありそうなものとして、横浜市の月別平均気温と月別平均相対湿度を回帰成分(外生変数)として準備する。
ソースは気象庁ホームページより。
なお本日使うパッケージはこれら。forecast でARIMAモデルを構築する。
library(tidyverse)
library(forecast)
データ加工
今回、簡便な方法として forecastパッケージの auto.arima 関数を使ってみる。
時系列データセットはTime-Series型、外生変数はmatrix型かvector型が要求されるため、ts関数とmatrix関数で型変換しておく。
FIRE <- read_csv("./yokohama_kasai.csv")
TEMP <- read.csv("./yokohama_kion.csv")
HUMI <- read.csv("./yokohama_shitsudo.csv")
ADTS <- ts(FIRE$火災件数, frequency=12)
ADXREG <- as.matrix(data.frame(TEMP=TEMP$平均気温, HUMI=HUMI$平均湿度), col=12)
また、17年分(2000~2016年)を学習期間、3年(2017~2019年)をテスト期間としてみる(ホールドアウト法)。
データ分割はwindow関数で比較的簡単にできる。
ADTS.train <- window(ADTS, c( 1, 1), c(17,12))
ADTS.test <- window(ADTS, c(18, 1), c(20,12))
nt <- length(ADTS.train)
ADXREG.train <- window(ADXREG, 1, nt)
ADXREG.test <- window(ADXREG, nt+1, 240)
観測値の時系列の描画
auto.arima関数を使う前に観測値の時系列を見てみる。
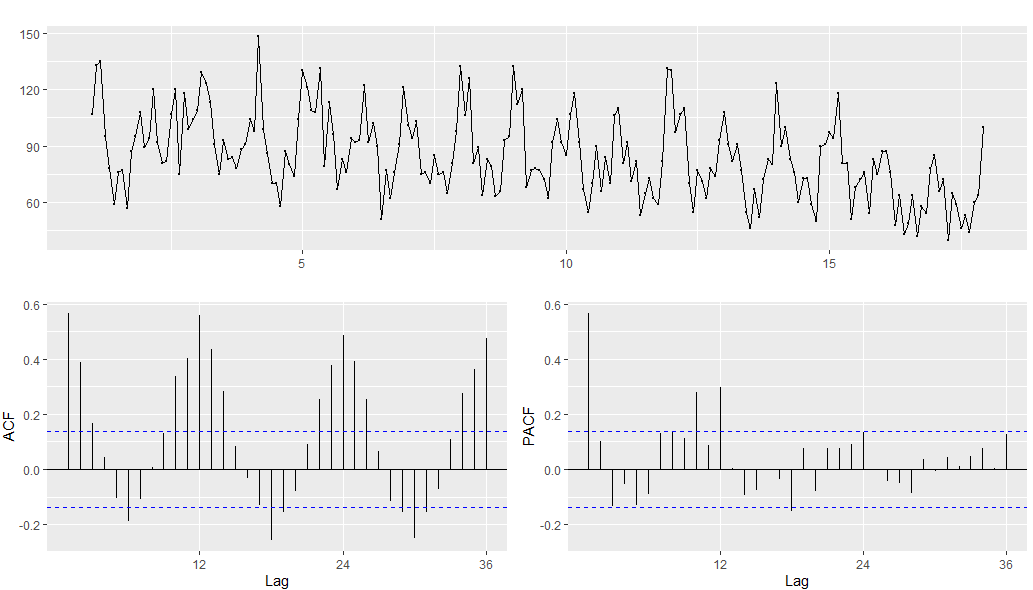
forecast::ggtsdisplay関数を使うと時系列、自己相関、偏自己相関をさっとグラフ化してくれる。
グラフから今回のデータにはラグ1~3の自己相関、1年くらいの季節周期がありそうだと分かる。
forecast::ggtsdisplay(ADTS.train)
単位根の検定
ARは定常過程を前提とするため、まず単位根を確認してみる。
urcaパッケージが有名なようだが、forecastパッケージでも ndiffs関数でADF検定やKPSS検定などの単位根検定ができるため、今回はforecastパッケージに統一する。ndiffs関数は、戻り値として d階差がいくつかを返してくれるシンプルなもの。
ADF検定は、帰無仮説を「単位根過程である」、対立仮設を「単位根はない」とし、帰無仮説が棄却されなければ単位根があると解釈する手法のようである。
一方、KPSS検定はその逆で、帰無仮説を「単位根がない」とし、棄却されれば単位根があるとする。
forecast::ndiffs(ADTS.train, test="adf")
forecast::ndiffs(ADTS.train, test="kpss")
悩ましいことに、今回のデータではADF検定で単位根なし、KPSS検定で単位根ありとなった。今回はauto.arima関数のデフォルトであるKPSS検定に従うとする。
ARIMAモデルの実行
前述のとおり、forecastパッケージのauto.arima関数を用いる。
先ずは季節成分なし(seasonal=F)でARIMAモデルを実行する。
先ほど単位根検定を行ったが、auto.arima関数内で d=NAとすると単位根検定を行い、d階差を調べてくれるため、試しがてらNAにする。
なお、stepwise=FALSEにすると総当たりでベストモデルを探してくれるようなので今回はFALSEにする(計算コストはかかるが・・)。他、処理速度を上げるため、並列処理(parallel=TURE)にし、CPUのコア数は8とした(ここは自前のPCと要相談)。
mod.arima <- forecast::auto.arima(ADTS.train
,d = NA
,start.p = 0
,start.q = 0
,seasonal = F
,stepwise = F
,parallel = T
,num.cores = 8
)
auto.arimaを実行するとあっけないほど簡単にモデルが作成できる。
今回はARIMA(3,1,2)がベストモデルとなった。



> summary(mod.arima)
Series: ADTS.train
ARIMA(3,1,2)
Coefficients:
ar1 ar2 ar3 ma1 ma2
1.1245 -0.1420 -0.2988 -1.6998 0.7290
s.e. 0.0883 0.1098 0.0737 0.0680 0.0643
sigma^2 estimated as 288: log likelihood=-861.58
AIC=1735.17 AICc=1735.6 BIC=1755.05
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set -1.726492 16.71896 13.4789 -6.19378 17.2469 0.9039288 -0.04407495
次に作成モデルの残差診断を行う。モデルが適切であれば、残差は定常であり自己相関がない。
forecastパッケージでは、checkresiduals関数で残差診断が可能であり、リュング・ボックス検定(Ljung-Box test)を行ってくれる。
この検定は、帰無仮説を「自己相関がない」、対立仮設を「少なくとも1つ以上のラグに自己相関がある」とし、帰無仮説が棄却されなければ自己相関がないと解釈する手法である。
今回は p<0.001で有意であり、自己相関がないとは言えない。checkresiduals関数で出力されるコレログラムを見ると自己相関がありそうだと見て取れる。
> resid.arima <- forecast::checkresiduals(mod.arima)
Ljung-Box test
data: Residuals from ARIMA(3,1,2)
Q* = 57.292, df = 19, p-value = 1.029e-05
Model df: 5. Total lags used: 24

なお、ARIMAモデルでの予測は次のとおり(黒:観測値、青:予測値)。
fig.arima <- ggplot() +
geom_line(mapping=aes(x=1:length(mod.arima$fitted), y=c(mod.arima$x)), color="black", size=1) +
geom_line(mapping=aes(x=1:length(mod.arima$fitted), y=c(mod.arima$fitted)), color="blue", size=2, alpha=.4) +
labs(title=gsub("Residuals from ","",resid.arima$data.name), x="", y="") +
theme(plot.title=element_text(size=30)
,axis.title=element_text(size=25)
,axis.text=element_text(size=20))
plot(fig.arima)

SARIMAモデルの実行
続いて、SARIMAを試してみる。
auto.arima を seasonal = T にすることで季節を考慮できる。
なお、季節周期を組み込む場合、入力データにあらかじめ周期を持たせておく必要がある。今回は、ts(FIRE$火災件数, frequency=12) で12周期としている。
mod.sarima <- forecast::auto.arima(ADTS.train
,d = NA
,D = NA
,start.p = 0
,start.q = 0
,start.P = 0
,start.Q = 0
,seasonal = T
,stepwise = F
,parallel = T
,num.cores = 8
)
今回はSARIMA(1,0,1)(0,1,1)[12] がベストモデルであった。








> summary(mod.sarima)
Series: ADTS.train
ARIMA(1,0,1)(0,1,1)[12]
Coefficients:
ar1 ma1 sma1
0.9644 -0.7851 -0.8848
s.e. 0.0586 0.1284 0.0847
sigma^2 estimated as 201.2: log likelihood=-788.79
AIC=1585.57 AICc=1585.79 BIC=1598.6
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set -1.322366 13.65188 10.26076 -3.751509 12.7082 0.6881126 0.08705428
また、リュング・ボックス検定(Ljung-Box test)は非有意であり、自己相関がないと解釈する。コレログラムを見ても自己相関はなくなったようである。
> resid.sarima <- forecast::checkresiduals(mod.sarima)
Ljung-Box test
data: Residuals from ARIMA(1,0,1)(0,1,1)[12]
Q* = 18.737, df = 21, p-value = 0.602
Model df: 3. Total lags used: 24

SARIMAモデルでの予測は次のとおり(黒:観測値、青:予測値)。
fig.sarima <- ggplot() +
geom_line(mapping=aes(x=1:length(mod.sarima$fitted), y=c(mod.sarima$x)), color="black", size=1) +
geom_line(mapping=aes(x=1:length(mod.sarima$fitted), y=c(mod.sarima$fitted)), color="blue", size=2, alpha=.4) +
labs(title=gsub("Residuals from ","",resid.sarima$data.name), x="", y="") +
theme(plot.title=element_text(size=30)
,axis.title=element_text(size=25)
,axis.text=element_text(size=20))
plot(fig.sarima)

SARIMAXモデルの実行
続いて続いて、回帰成分を入れてSARIMAXモデルを試してみる。
auto.arima に xreg = 回帰成分のデータ とすることで天候情報を加える。
平均気温のみ、相対湿度のみ、平均気温&相対湿度の計3パターンのモデルを作ってみるが、以降の例は平均気温のみのモデルで説明する。
mod.sarimax1 <- forecast::auto.arima(ADTS.train
,d = NA
,D = NA
,start.p = 0
,start.q = 0
,start.P = 0
,start.Q = 0
,seasonal = T
,xreg = ADXREG.train[,1]
,stepwise = F
,parallel = T
,num.cores = 8
)
auto.arimaの結果、回帰成分を含めた ARIMA(1,1,2)(2,0,0)[12] がベストモデルとなった。




Series: ADTS.train
Regression with ARIMA(1,1,2)(2,0,0)[12] errors
Coefficients:
ar1 ma1 ma2 sar1 sar2 xreg
0.7233 -1.5227 0.5386 0.2089 0.1610 -1.6775
s.e. 0.1987 0.2304 0.2188 0.0718 0.0744 0.2372
sigma^2 estimated as 221.3: log likelihood=-834.48
AIC=1682.95 AICc=1683.53 BIC=1706.15
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set -1.544109 14.61906 11.72934 -4.971464 14.77754 0.7865994 0.003945916
また、リュング・ボックス検定(Ljung-Box test)は非有意であり、自己相関がないと解釈する。コレログラムを見ても自己相関はなさそうである。
> resid.sarimax1 <- forecast::checkresiduals(mod.sarimax1)
Ljung-Box test
data: Residuals from Regression with ARIMA(1,1,2)(2,0,0)[12] errors
Q* = 16.162, df = 18, p-value = 0.5812
Model df: 6. Total lags used: 24

なお、SARIMAXモデルでの予測は次のとおり(黒:観測値、青:予測値)。
fig.sarimax1 <- ggplot() +
geom_line(mapping=aes(x=1:length(mod.sarimax1$fitted), y=c(mod.sarimax1$x)), color="black", size=1) +
geom_line(mapping=aes(x=1:length(mod.sarimax1$fitted), y=c(mod.sarimax1$fitted)), color="blue", size=2, alpha=.4) +
labs(title=gsub("Residuals from ","",resid.sarimax1$data.name), x="", y="") +
theme(plot.title=element_text(size=30)
,axis.title=element_text(size=25)
,axis.text=element_text(size=20))
plot(fig.sarimax1)

モデルの比較
以上、ARIMA、SARIMA、SARIMAX(平均気温のみ、相対湿度のみ、平均気温&相対湿度)の5モデルを試してみた。
このうち、残差診断で自己相関がないと解釈できたSARIMAとSARIMAXの2つを中心にどっちが良いか考えてみる。
1つの指標としてAICを見比べてみると、SARIMAモデルが良好のようである。
>
> mod.arima$aic
[1] 1735.168
> mod.sarima$aic
[1] 1585.574
> mod.sarimax1$aic
[1] 1682.954
> mod.sarimax2$aic
[1] 1607.806
> mod.sarimax3$aic
[1] 1603.069
ただし、AICは長期予測の評価に不向きのようなので、準備していたテストデータを用いて予測値と実測値の差を評価する。
ということで、作成モデルでテスト期間の予測を行う。
予測は forecast::forecast関数で行う。hで予測期間、xregで回帰成分を指定する。
> pred.arima <- forecast::forecast(mod.arima, h=36)
> pred.sarima <- forecast::forecast(mod.sarima, h=36)
> pred.sarimax1 <- forecast::forecast(mod.sarimax1, h=36, xreg=ADXREG.test[,1])
> pred.sarimax2 <- forecast::forecast(mod.sarimax2, h=36, xreg=ADXREG.test[,2])
> pred.sarimax3 <- forecast::forecast(mod.sarimax3, h=36, xreg=ADXREG.test)
予測ができたらforecast::accuracy関数でテスト期間の予実の差を評価する。
以下は見やすさのため round で丸めている。
> round(forecast::accuracy(pred.arima, ADTS.test), 3)
ME RMSE MAE MPE MAPE MASE ACF1 Theils U
Training set -1.726 16.719 13.479 -6.194 17.247 0.904 -0.044 NA
Test set -1.211 13.147 10.879 -6.628 19.018 0.730 0.365 0.943
> round(forecast::accuracy(pred.sarima, ADTS.test), 3)
ME RMSE MAE MPE MAPE MASE ACF1 Theils U
Training set -1.322 13.652 10.261 -3.752 12.708 0.688 0.087 NA
Test set -10.897 17.996 15.191 -20.715 26.342 1.019 -0.010 1.168
> round(forecast::accuracy(pred.sarimax1, ADTS.test), 3)
ME RMSE MAE MPE MAPE MASE ACF1 Theils U
Training set -1.544 14.619 11.729 -4.971 14.778 0.787 0.004 NA
Test set -3.952 12.655 11.232 -9.038 19.146 0.753 0.040 0.839
> round(forecast::accuracy(pred.sarimax2, ADTS.test), 3)
ME RMSE MAE MPE MAPE MASE ACF1 Theils U
Training set -1.218 12.351 9.413 -3.579 11.73 0.631 0.044 NA
Test set -6.153 13.265 10.371 -10.731 16.95 0.696 0.346 0.771
> round(forecast::accuracy(pred.sarimax3, ADTS.test), 3)
ME RMSE MAE MPE MAPE MASE ACF1 Theils U
Training set -1.295 12.145 9.311 -3.630 11.646 0.624 0.006 NA
Test set -7.307 13.918 11.066 -12.473 18.296 0.742 0.303 0.815
実測値ベースで良く使われる指標としては、RMSE(Root Mean Square Error、二乗平均平方根誤差)やMAE(Mean Absolute Error、平均絶対誤差)がある。


RMSEもMAEも予実の差を見ているが、RMSEは二乗、MAEは絶対値を用いるため異常値に対する重みが違う。
異常値を厳しくみたいのであればRMSEの方が良いが、時系列に処理できないスパイクが複数出てしまうのであれば、MAEの方が実感にあうかもしれない。
また、相対的な指標(割合ベースの指標)としては、MAPE(Mean Absolute Percentage Error、平均絶対誤差率)やMASE(Mean Absolute Scaled Error、平均絶対尺度誤差)がある。
例えば横浜市だけでなく川崎市・茅ヶ崎市など別地点のモデルとも比較したいのであれば、実測値ベースの評価指標では比較できないため、相対的な指標を用いると良い。


MAPEは予実の差を実測値で割る性質から実測値 ≧ 予測値の時
![[0,\ 1]](https://chart.apis.google.com/chart?cht=tx&chl=%20%5B0%2C%5C%201%5D)
、実測値 ≦ 予測値の時
![[ 0,\infty ]](https://chart.apis.google.com/chart?cht=tx&chl=%20%5B%200%2C%5Cinfty%20%5D)
の範囲をとり、予測の上振れに大きく反応する。また、実測値に0があると割り算できず使用できない。
MASEは過去時点との差を分母にとる方法で「ナイーブな方法」と言われる。過去時点 m はラグ1や季節周期を用いる。過去時点でスケーリングするため、
過学習に注意が必要となる。MAPEと異なり 0 があっても良い。
今回、MAPE・MASEで評価すると平均相対湿度を回帰成分にしたSARIMAXモデルが最も良好だった。
ただし、原系列の下降トレンドをうまく表現するために、人口構成なり住居特性の変化なり何かしら構造的な説明変数を組み込むことで更なる改善が期待される。
なお、ARIMA、SARIMA、SARIMAXの予測線を並べると次のようになった。
ggplot() +
geom_line(mapping=aes(x=128:240, y=c(ADTS[128:240])), color="black", size=1) +
geom_line(mapping=aes(x=(nt+1):240, y=c(pred.arima$mean), color="arima1"), size=2, alpha=.4) +
geom_line(mapping=aes(x=(nt+1):240, y=c(pred.sarima$mean), color="arima2"), size=2, alpha=.4) +
geom_line(mapping=aes(x=(nt+1):240, y=c(pred.sarimax1$mean), color="arima3"), size=2, alpha=.4) +
geom_line(mapping=aes(x=(nt+1):240, y=c(pred.sarimax2$mean), color="arima4"), size=2, alpha=.6) +
geom_line(mapping=aes(x=(nt+1):240, y=c(pred.sarimax3$mean), color="arima5"), size=2, alpha=.6) +
labs(x="", y="", title="予測:モデル比較") +
scale_colour_manual(
name="モデル"
,values=c(arima1="blue", arima2="darkgreen", arima3="red", arima4="orange", arima5="gray")
,labels=c("ARIMA","SARIMA","SARIMAX\n(気温)","SARIMAX\n(湿度)","SARIMAX\n(気温&湿度)")) +
scale_x_continuous(breaks=seq(128,240,by=12), labels=c(2010:2019)) +
theme(plot.title=element_text(size=25)
,axis.text=element_text(size=20)
,legend.title=element_text(size=23)
,legend.text=element_text(size=20))

おわりに
以上、ARIMAモデル系をRで試してみた。
とは言っても auto.arima を使った簡易的な方法である。時系列分析は職人技と耳にしたことがあるが、最適なパラメータの設計はまさにそうなのだと思う。
また、回帰成分も簡単に入手できる天気のみにしたが、カレンダー効果、人口構造、木造・鉄筋の割合、耐火技術、天災、制度変更など他にも意味のある変数が考えられる。
SASでの実行は余力があるときにまた。
参考
Forecasting: Principles and Practice (2nd ed)
6.7 Prediction accuracy | Fisheries Catch Forecasting
http://www.ide.titech.ac.jp/~hanaoka/finalversion-of-conference.pdf
ExploratoryでProphetを使って時系列予測してみた(後編) | Tableau-id Press -タブロイド-
利用データ
月別火災発生件数 横浜市
気象庁|過去の気象データ・ダウンロード
※本ブログで作成したグラフ等は、上記「利用データ」を編集・加工して作成しています。本分析は解析方法・プログラミングの学習を目的としており、提案・提言等を行うものではありません。