【統計】ロジスティック回帰分析

ロジスティック回帰分析について。

【目次】

今回はモデル作成まで。モデルの評価は別記事で。

計算式等

---

ロジスティック回帰は二値分類（）で用いられる分析手法。
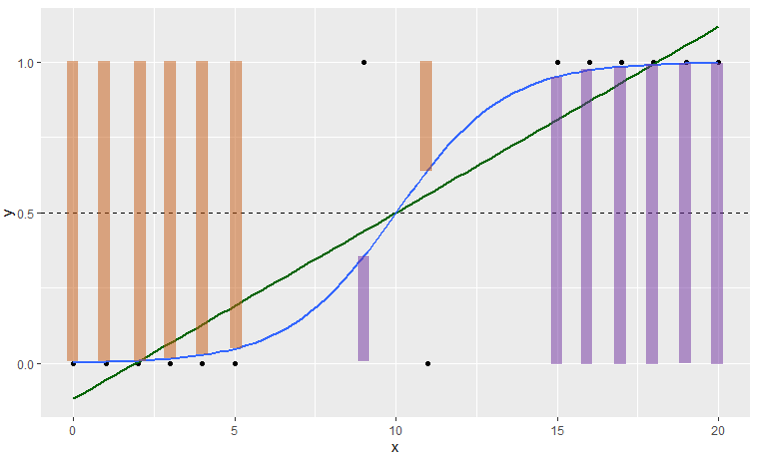
モデル式は回帰分析と似ているが、シグモイド関数を使って０～１の範囲の結果を出すことが特徴（通常の回帰分析では０～１の範囲を超えてしまい、解釈不能な結果になってしまう）。
（青線：ロジスティック回帰、緑線：単回帰分析）

モデル式、シグモイド関数および損失関数はそれぞれ次のとおり。

モデル式

シグモイド関数（活性化関数）

交差エントロピー誤差（分類問題の損失関数）

　※ ln( ) は自然対数。 は実測値で です（正解ラベルとも言われます）。

交差エントロピー誤差は、対数尤度にマイナスをつけて０を最小値としたもの（負の対数尤度）。式の第一項（  ）で実際にイベントが起きたデータ（  ）に対する予測誤差を計算する（予測90%なら10%が誤差）。式の第二項（  ）でイベントが起きなかったデータ（  ）に対する予測誤差を計算する（予測10%なら10%が誤差）。
第一項も第二項も  の時に  となることから、実測値と予測値が完全一致すれば合計０で誤差なしとなる。
※イメージ的には紫の棒が の時の 、オレンジの棒が の時の 。

対数尤度関数の計算方法についても掲載。
対数尤度関数

尤度関数

※尤度関数は０～１の確率を "かけ算" するため、値がかなり小さくなってしまう（コンピュータ計算に不向き）。そのため、対数変換して確率の "足し算" とした対数尤度関数が広く使われる。

そして、肝心の回帰係数 β の計算方法は次のとおり。
回帰係数 β の計算方法

式中に  があるため、"回帰係数 β を算出するために回帰係数 β が必要" ということになる。本記事ではニュートン・ラフソン法（以降、ニュートン法）による回帰係数の更新方法を取り上げる。

ニュートン法

ニュートン法では既存の回帰係数  と演算後の回帰係数 との差がなくなるまで更新を繰り返す。最適解の算出には交差エントロピー誤差のヘッセ行列（H）と重み付き行列（R）を用いる。このRはシグモイド関数の微分の対角行列。

これらをまとめると次の図解。

近似的な方法

簡易的にロジスティック回帰分析を行う方法として、ロジット変換した値を目的変数にした回帰分析がある。二値を Yes / No の数で表すとロジット変換は次の式。

なお、０の対数変換 は計算できないため、0.5 を加算してロジット変換する方法がある。これを経験ロジットと言う。 

また、この回帰分析に重みを加えたい場合、ロジットの分散の逆数を重みとする（重み付き回帰分析）。経験ロジットを使う場合は３つ目の式。

最後に、覚えておくと良さそうなシグモイド関数の性質をメモ。

シグモイド関数の性質


　←オッズ比

ノート

---

今回も簡単なデータで計算手順を見てみる。

■ サンプルデータ

X1	X2	Nyes	Nall	Pyes	Logit	経験Logit
5	0	1	20	0.050	-2.944	-2.565
5	1	6	22	0.273	-0.981	-0.932
10	0	9	25	0.360	-0.575	-0.552
10	1	16	30	0.533	0.134	0.129
15	0	19	30	0.633	0.547	0.528
15	1	28	30	0.933	2.639	2.434

今回は近似的な方法で算出した回帰係数 β を初期値にする
その後、ニュートン法を用いて回帰係数 β を更新し、最適解を探す。

初期値設定 

LINEST関数で計算。目的変数は経験ロジット。今回は重み付き回帰分析はしていない（単に初期値を得るためなので）。
回帰係数 β はそれぞれ  。
※LINEST関数の使い方は単回帰分析で記載。

cochineal19.hatenablog.com

回帰係数 β の更新１回目 

初期値の回帰係数 β をもとに予測値  を算出する。
サンプルデータの１行目は なので次のとおり。※上図Excel A列の は切片項用に 1 を設定。

次にヘッセ行列を求める。
＜式の再掲＞

サンプルデータの１行目を取り上げると R は 。
ヘッセ行列は次のとおりで、今回は切片＋説明変数２つの３次元なので３×３の行列になる。

 

※ 今回の集計表はレコードをまとめているため、計算式に「 」を入れている。

さらに  を求める。

※ 今回の集計表はレコードをまとめているため、計算式に「 」と「 」を入れている。「 」は の時だけ０以外の値を持つため「 」としている。 

これら計算結果から回帰係数 β を更新すると次のようになる。

 それぞれの更新前後の差は 0.00306, 0.00198, 0.08494 で差があるので更新を続ける。

回帰係数 β の更新２回目 

更新２回目は  で更新前後の差は 0.00508, -0.00043, -0.00206 。だいぶ良くなったが、まだ差があるので更新する。

回帰係数 β の更新３回目 

更新３回目は  で更新前後の差は 0.000000, 0.000000, 0.000000 。更新前後の回帰係数 β が同値で差がなくなった。

よって更新はここまでにして次を最終モデルとする。

Rでの実行：

> ads <- data.frame(
+   x1=c(rep(5,20),rep(5,22),rep(10,25),rep(10,30),rep(15,30),rep(15,30))
+   ,x2=c(rep(0,20),rep(1,22),rep(0,25),rep(1,30),rep(0,30),rep(1,30))
+   ,y=c(rep(0,19),rep(1,1),rep(0,16),rep(1,6),rep(0,16),rep(1,9),rep(0,14),rep(1,16),rep(0,11),rep(1,19),rep(0,2),rep(1,28))
+ )
> fit1 <- glm(y ~ x1 + x2, family=binomial, data=ads)
> summary(fit1)
Call:
glm(formula = y ~ x1 + x2, family = binomial, data = ads)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.0812  -0.8307   0.4935   0.8906   2.2684  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -4.10022    0.72055  -5.690 1.27e-08 ***
x1           0.32135    0.05562   5.778 7.58e-09 ***
x2           1.32386    0.40344   3.281  0.00103 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)
    Null deviance: 217.64  on 156  degrees of freedom
Residual deviance: 164.56  on 154  degrees of freedom
AIC: 170.56
Number of Fisher Scoring iterations: 4

SASでの実行：

data ads(drop=i);
  do i=1 to  1; x1= 5; x2=0; y=1; output; end;
  do i=1 to 19; x1= 5; x2=0; y=0; output; end;
  do i=1 to  6; x1= 5; x2=1; y=1; output; end;
  do i=1 to 16; x1= 5; x2=1; y=0; output; end;
  do i=1 to  9; x1=10; x2=0; y=1; output; end;
  do i=1 to 16; x1=10; x2=0; y=0; output; end;
  do i=1 to 16; x1=10; x2=1; y=1; output; end;
  do i=1 to 14; x1=10; x2=1; y=0; output; end;
  do i=1 to 19; x1=15; x2=0; y=1; output; end;
  do i=1 to 11; x1=15; x2=0; y=0; output; end;
  do i=1 to 28; x1=15; x2=1; y=1; output; end;
  do i=1 to  2; x1=15; x2=1; y=0; output; end;
run;

ods output LackFitChiSq=HOSLEM1;
proc logistic data=ads descending;
  model y(event='1') = x1 x2 / outroc=ROC1 lackfit;
  output out=OutDS;
run;

統計ソフトってすごく便利。。と体感した。

プログラムコード

---

■ Rのコード

fit <- glm(y ~ x1 + x2, family=binomial, data=ads)
summary(fit)

■ SASのコード

proc logistic data=[InputDS] descending;
  model y(event='1') = x1 x2;
  output out = [OutDS];
run; quit;

■ Pythonのコード

整備中

交差エントロピー誤差の偏微分

---

回帰係数 β の計算方法で示した交差エントロピー誤差の偏微分の詳細。
「連鎖律」という方法で微分する。

交差エントロピー誤差

偏微分

図解するとこんな感じ。シグモイド関数の微分は公式で z(1-z) になる。

 

-----

なお、SASやRのロジスティック回帰では「ニュートン法」ではなく、「フィッシャースコアリング法」が用いられているようだった（記事を書き終わってから気づいた）。
この方法は、ニュートン法で使った「ヘッセ行列」を「フィッシャー情報行列」に置き換えたもの。計算コストが良い様子。
今回は更新の仕組みが分かれば良いと思っていたため、この記事は終了。

フィッシャースコアリング法について Wikipedia を参照。

尤度方程式 - Wikipedia

参考

---

統計学（出版：東京図書）, 日本統計学会編

多変量解析実務講座テキスト, 実務教育研究所

統計学入門−第10章

PRML4.3.3

---

★サイトマップ

cochineal19.hatenablog.com

【統計】重回帰分析

重回帰分析について。

【目次】

単回帰分析については次の記事。

cochineal19.hatenablog.com  

計算式等

---

重回帰分析は、多変量 {  } の関係を直線で求める分析方法。
モデルは次のとおり。

■ 重回帰モデル

■ 重回帰式

は切片（intercept）、 は回帰係数（regression coefficient）であり、回帰係数は x が１増えた時に y がどのくらい増えるかを表す。
回帰係数の式は、「回帰係数」＝「説明変数間の分散共分散行列の逆行列」×「説明変数と目的変数の共分散行列」。

なお、正規方程式から次のように回帰係数を求めることもできる。


　※X：説明変数の行列、Y：目的変数の行列、β：回帰係数の行列、t：転置

また、説明変数で表現できないものを残差 と言い、この残差は互いに独立に正規分布 に従う。

重回帰分析は分散分析表で表現することができる。
この分散分析表は単回帰分析で示したものと同じ。

■ 分散分析表

変動因	平方和	自由度	平均平方	F比
回帰R
残差e
全体T

　k=説明変数の数

なお、平方和と自由度は  の関係が成り立つ。

モデルの評価指標としては次のようなものがある（一例）。

寄与率もしくは決定係数（R-square）

　0～1の値を取り、1に近いほど良い。 

自由度調整済寄与率もしくは自由度調整済決定係数（adjusted R-square）

　0～1の値を取り、1に近いほど良い。

RMSE（Root Mean Square Error, 二乗平均平方根誤差）

　相対的な指標であり、値が小さいほど良い。予測値と実測値の誤差に関する指標。

AIC（Akaike's Information Criterion, 赤池情報量規準）

　　※ MLL : 最大対数尤度（Maximum Log Likelihood）, k : 説明変数の数
　相対的な指標であり、値が小さいほど良い。2×(k) が説明変数の数に対する罰則項である。

VIF（Variance Inflation Factor, 分散拡大係数）

　　※ r : 相関係数
　多重共線性の評価に用いる。目安として10以上で多重共線性があると考える。

ノート

---

今回も架空データで簡単に計算方法を見てみる。

　x1 = {1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3}
　x2 = {2, 1, 1, 2, 1, 3, 4, 2, 4, 3, 3, 6, 6, 4, 5}
　x3 = {5, 6, 5, 2, 3, 5, 7, 5, 4, 6, 5, 9, 6, 5, 5}
　x4 = {2, 1.5, 2, 2, 1.5, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4}
　y = {1.1, 2.4, 3.3, 2.5, 1.3, 3.1, 2.7, 4.9, 2.4, 3.5, 5.8, 4.4, 3.1, 4.9, 5.3}

Excelでの計算：

重回帰分析

モデルの作成

分散共分散行列と逆行列は次のとおり。

 

よって、今回の重回帰式は次のとおり。

モデルの評価

今回の結果についてVIFを調べてみると x1=38.2,  x2=4.3,  x3=1.5,  x4=40.2 であり、x1 と x4 に多重共線性が疑われる（VIF≧10を目安）。x1 と x4 は相関係数=0.987 であり、かなり強い相関関係がある様子。
したがって、x1 と x4 の一方を外したモデルを作って再評価してみる。また、x3 が非有意（p>0.05）だったため、x3 を外したモデルも作ってみる。
（※この記事では変数選択の手法には触れない。）

＜評価モデル＞
　res1 : y = x1 + x2 + x3 + x4
　res2 : y = x1 + x2 + x3
　res3 : y = x2 + x3 + x4
　res4 : y = x1 + x2
　res5 : y = x2 + x4

実行結果は次のとおり。

	res1	res2	res3	res4	res5
VIF≧10	あり	なし	なし	なし	なし
R2	0.853	0.812	0.849	0.808	0.839
adj R2	0.794	0.761	0.808	0.776	0.812
RMSE	0.643	0.692	0.620	0.670	0.613
AIC	35.256	36.873	33.573	35.192	32.558

x1 と x4 の一方を外すことで VIF≧10 の変数は無くなり、多重共線性の問題が解消されたと考えられる。
また、自由度調整済寄与率 の最大値、RMSEとAICの最小値は何れも res5 であり、今回は res5: y=x2 + x4 が最良モデルと考えられる。
なお、res5のモデルは統計的に有意であり（p<0.001）、各回帰係数も有意（x2: p<0.05, x4: p<0.001）。
※今回のモデル比較では、説明変数の数が異なるため、寄与率は は使わず、自由度調整済寄与率 を評価指標としている。

Rでの実行

> ads <- data.frame(x1  = c(1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3)
+                   ,x2 = c(2, 1, 1, 2, 1, 3, 4, 2, 4, 3, 3, 6, 6, 4, 5)
+                   ,x3 = c(5, 6, 5, 2, 3, 5, 7, 5, 4, 6, 5, 9, 6, 5, 5)
+                   ,x4 = c(2, 1.5, 2, 2, 1.5, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4)
+                   ,y  = c(1.1, 2.4, 3.3, 2.5, 1.3, 3.1, 2.7, 4.9, 2.4, 3.5, 5.8, 4.4, 3.1, 4.9, 5.3))
> res1 <- lm(y ~ x1 + x2 + x3 + x4, data=ads)
> summary(res1)
Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = ads)

Residuals:
    Min      1Q  Median      3Q     Max 
-0.8829 -0.3648 -0.2275  0.4359  0.9455 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) -1.16286    1.11986  -1.038  0.32354   
x1           0.58168    1.25690   0.463  0.65342   
x2          -0.87065    0.21243  -4.099  0.00215 **
x3           0.09705    0.12824   0.757  0.46665   
x4           1.91008    1.15667   1.651  0.12968   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.6434 on 10 degrees of freedom
Multiple R-squared:  0.8525,	Adjusted R-squared:  0.7935 
F-statistic: 14.45 on 4 and 10 DF,  p-value: 0.0003674

> AIC(res1)
[1] 35.25556
> vif(res1)
       x1        x2        x3        x4 
38.165148  4.331555  1.446171 40.185695 

#他のモデル
# res2 <- lm(y ~ x1 + x2 + x3, data=ads)
# res3 <- lm(y ~ x2 + x3 + x4, data=ads)
# res4 <- lm(y ~ x1 + x2, data=ads)
# res5 <- lm(y ~ x2 + x4, data=ads)

SASでの実行

data ads;
input x1 x2 x3 x4 y @@;
cards;
1 2 5 2 1.1 1 1 6 1.5 2.4 1 1 5 2 3.3 1 2 2 2 2.5 1 1 3 1.5 1.3
2 3 5 3 3.1 2 4 7 3 2.7 2 2 5 3 4.9 2 4 4 3 2.4 2 3 6 3 3.5
3 3 5 4 5.8 3 6 9 4 4.4 3 6 6 4 3.1 3 4 5 4 4.9 3 5 5 4 5.3
;run;
proc reg data=ads;
 model y = x1 x2 x3 x4 / SELECTION=ADJR RSQUARE AIC RMSE VIF;
run;

プログラムコード

---

■ Rのコード

library(car)
res <- lm(y ~ x1 + x2, data=InputDS)
summary(res)
vif(res) #-- VIFを算出
AIC(res) #-- AICを算出

■ SASのコード

ods listing close;
ods output SubsetSelSummary=OutputSummary; /* 全変数パターンの評価指標値を取得 */
proc reg data=[InputDS];
 model y = x1 x2 / selection=ADJR RSQUARE AIC RMSE VIF; /* VIFはmodelの式のみ */
 output out=[OutputDS] p=pred r=residuals; /* modelに書いた式での予測値・残差取得 */
run;quit;
ods listing;

■ Pythonのコード

整備中

偏回帰係数の詳細

---

の求め方についてもう少し突っ込んでみる。

精度の良いモデルとは、残差 が小さいモデルであるため、残差平方和が最小の時の を用いれば良いと考えられる（最小二乗法）。

したがって、 について偏微分した式を連立方程式にして最良値を求める。
　元：

　※合成関数の微分により、[n]×[関数^(n-1)]×[関数の中身の偏微分]。傾き最小を求めるので右辺は０。

ここから -2 を除去して変形すると次のようになり、

①を用いて、 を次の関係式で表すことができる。

この⑤を②に代入して、次の関係式を求める。

③④も同じ処理で次の関係式を求める。

これら⑥⑦⑧を行列表現すると次のようになり、

さらに変形して、各回帰係数の導出式を得る。

つまり、「回帰係数」＝「説明変数間の分散共分散行列の逆行列」×「説明変数と目的変数の共分散行列」。

よって、⑤⑨から  は次となる。

なお、分散共分散行列を相関行列にすると標準偏回帰係数が得られる。

・・・その他、
①②③④を行列表現すると次のようになり、この方程式からも回帰係数を導出できる（この方程式を「正規方程式」と言う）。
＜再掲＞

＜正規方程式・回帰係数の解＞


　※X：説明変数の行列、Y：目的変数の行列、β：回帰係数の行列、t：転置

Excelで計算する際は、①の切片項＝1（下図のA列）を与えて、公式通り計算。 

この方法だと、分析共分散行列を作らず、説明変数と目的変数を直接使って回帰係数を導出できる。 

参考

---

統計学（出版：東京図書）, 日本統計学会編

多変量解析実務講座テキスト, 実務教育研究所

市川伸一他, SASによるデータ解析入門 [第３版]（出版：東京大学出版会）

【統計】単回帰分析

単回帰分析について。

【目次】

計算式等

---

単回帰分析は、２変量 {x,y} の関係を直線（一次式）で求める分析方法。
モデル、式は次のとおり。

■ 単回帰モデル

■ 単回帰式

は切片（intercept）、 は回帰係数（regression coefficient）であり、回帰係数は x が１増えた時に y がどのくらい増えるかを表す。
また、説明変数で表現できないものを残差 と言い、この残差は独立に正規分布 に従う。

単回帰分析は次の分散分析表で表現することができる。
この分散分析表は一元配置分散分析で示したものと同じ。

■ 分散分析表

変動因	平方和	自由度	平均平方	F比
回帰R
残差e
全体T

　k=説明変数の数（単回帰分析では１）

なお、平方和と自由度は  の関係が成り立つ。

モデルの評価指標としては次のようなものがある（一例）。

寄与率もしくは決定係数（R-square）

　 
　0～1の値を取り、1に近いほど良い。

自由度調整済寄与率もしくは自由度調整済決定係数（adjusted R-square）

　
　0～1の値を取り、1に近いほど良い。

RMSE（Root Mean Square Error, 二乗平均平方根誤差）

　
　相対的な指標であり、値が小さいほど良い。予測値と実測値の誤差に関する指標。

ノート

---

今回も架空データで簡単に計算方法を見てみる。

　x = {1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3}
　y = {1.1, 2.4, 3.3, 2.5, 1.3, 3.1, 2.7, 4.9, 2.4, 3.5, 5.8, 4.4, 3.1, 4.9, 5.3}

Excelでの計算：

単回帰分析

モデルの作成

 となるため、 は次のようになる。

よって、今回の単回帰式は次のとおり。

グラフにしたもの。

この計算、ExcelのLINEST関数でも実行できるのでメモ（個人の興味）。
貼付したExcelではP4:Q8が該当箇所。

 =LINEST(目的変数の範囲, 説明変数の範囲, 切片項有無, 補正項有無)
 [引数]
　第１、２引数：特に迷わないと思います。単純なデータ指定です。
　第３引数：切片を推定したい場合TRUEとします。FALSEにすると切片＝０です。 
　第４引数：FALSEにすると回帰係数と切片のみを返し、TRUEにすると寄与率、F値、平方和等の情報も計算してくれます。
　※今回の例では第３、４引数は両方ともTRUEにしました。

LINEST関数は５行×２列（列数は切片＋説明変数の数）を範囲指定し、Ctrl + Shift + Enter で実行する。実行後、各セルに次の結果が得られる。

出力結果＜再掲＞	各セルの詳細
	回帰係数（b1） 切片項（b0） b1 の標準誤差 b0 の標準誤差 寄与率（R2） 誤差項 F値 残差自由度 回帰平方和（SR） 残差平方和（Se）

出力結果を見てみると  は手計算と同じ結果が得られている。
また、F＝18.9384（回帰自由度＝1、残差自由度=13）なので、p≒0.0007843となる（セルP12=F.DIST.RT(F値のセル, 1, 残差自由度のセル) ）。

なお、回帰係数÷標準誤差で t値を求め、p値≒0.0007843 を得ることができる（セルP10:11）。

モデルの評価

LINEST関数の結果で得られる寄与率は0.5930。

「寄与率＝回帰平方和÷全体平方和」の式から分かるように、寄与率は本モデルでデータ全体のどのくらいを説明できるかを示す指標（１に近いほど良い）。
今回のモデルでは６割近くを説明できているという解釈になる。

なお、寄与率は「実測値と予測値の相関係数の二乗」に一致する。

※寄与率は説明変数を増やすだけで大きくなってしまうため、その影響を考慮した指標として自由度調整済寄与率がある。

Rでの実行

> ads <- data.frame(x=c(1,1,1,1,1,2,2,2,2,2,3,3,3,3,3)
+   　　　　　　　　,y=c(1.1, 2.4, 3.3, 2.5, 1.3, 3.1, 2.7, 4.9, 2.4, 3.5, 5.8, 4.4, 3.1, 4.9, 5.3))
> res <- lm(y ~ x, data=ads)
> summary(res)
Call:
lm(formula = y ~ x, data = ads)

Residuals:
   Min     1Q Median     3Q    Max 
-1.570 -0.735  0.120  0.520  1.520 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   0.8000     0.6404   1.249 0.233580    
x             1.2900     0.2964   4.352 0.000784 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.9374 on 13 degrees of freedom
Multiple R-squared:  0.593,	Adjusted R-squared:  0.5617 
F-statistic: 18.94 on 1 and 13 DF,  p-value: 0.0007843

> #-- グラフはこちら
> ggplot(ads, aes(x=x, y=y)) + geom_point() + geom_smooth(method="lm", se=F)

SASでの実行

data ads;
input x y @@;
cards;
1 1.1 1 2.4 1 3.3 1 2.5 1 1.3 2 3.1 2 2.7 2 4.9 2 2.4 2 3.5 3 5.8 3 4.4 3 3.1 3 4.9 3 5.3
;
run;
proc reg data=ads;
 model y = x;
 output out=OutputDS p=pred r=resid;
run;

プログラムコード

---

■ Rのコード

res <- lm(y ~ x, data=InputDS)
summary(res)

■ SASのコード

proc reg data=[InputDS];
 model y = x;
 output out=[OutputDS] p=pred r=residuals;
run;

■ Pythonのコード

整備中

回帰係数の詳細

---

の求め方についてもう少し突っ込んでみる。
精度の良いモデルとは、実測値 と予測値 との差（残差 ）が小さいものであるため、残差平方和が最小の時の を用いれば良いと考えられる（最小二乗法）。

最小値のイメージ

よって、 について偏微分した式を連立方程式にして最良値を求める。
上のイメージのように、残差平方和は二乗のため放物線の形をとり、傾き＝０が最小値となる。
　元：

　※合成関数の微分により、[n]×[関数^(n-1)]×[関数の中身の偏微分]。傾き最小を求めるので右辺は０。

ここから -2 を除去すると、具体的な名称として「残差の合計」と「残差×説明変数の合計」が０になる解を求めることが分かる。

この連立方程式を変形すると次のようになり、
 

①の式を用いて、 を次の関係式で表すことができる。

この③を②に代入すると が次のように求まる。

よって、③と④から は次となる。

参考

---

統計学（出版：東京図書）, 日本統計学会編

多変量解析実務講座テキスト, 実務教育研究所

市川伸一他, SASによるデータ解析入門 [第３版]（出版：東京大学出版会）

【統計】連関係数（ファイ、ピアソン、クラメール）

クロス表の連関係数について記載。

【目次】

計算式等

---

次のクロス表で考える。

		Outcome		Total
		0	1
Factor	1	a	b	AB
	2	c	d	CD
Total		AC	BD	N

ファイ係数（Phi coefficient）

　-1～１の値を取り、絶対値が１に近いほど関連性が大きい。
　２×２のクロス表で用いられ、本係数の絶対値はクラメールの連関係数と一致する。

ピアソンの連関係数 （Pearson's contingency coefficient）または一致係数

　※ は連続修正なしの値を用いる。

　０～１の値を取り、１に近いほど関連性が大きい。

クラメールの連関係数（Cramer's contingency coefficient）またはクラメールのV（Cramer's V）

　※min(R, C)はmin(行数, 列数)であり、行数と列数から最小値を取得する。
　※ は連続修正なしの値を用いる。

　０～１の値を取り、１に近いほど関連性が大きい。

カイ二乗統計量の計算は以下の記事。

【統計】χ二乗検定 - こちにぃるの日記

計算例

---

今回は２×２と３×３のクロス表で各係数を見てみる。
 

２×２のクロス表 

ファイ係数：

ピアソンの連関係数：

クラメールの連関係数：

Rでの実行：

> library(vcd)
> mtx1 <- matrix(c(30, 18, 10, 25), nrow=2, byrow=TRUE)
> vcd::assocstats(mtx1)
                    X^2 df  P(> X^2)
Likelihood Ratio 9.5650  1 0.0019832
Pearson          9.3323  1 0.0022515
Phi-Coefficient   : 0.335 
Contingency Coeff.: 0.318 
Cramer's V        : 0.335 

 SASでの実行： 

data ads;
input FACTOR OUTCOME CNT @@;
datalines;
1 0 30 1 1 18 2 0 10 2 1 25
;
run;
proc freq data=ads;
  table FACTOR * OUTCOME / chisq nocol nopercent;
  weight CNT / zeros;
  output out=Outds chisq;
run;

３×３のクロス表（２×２以上のクロス表）

ファイ係数：

　NA

ピアソンの連関係数：

クラメールの連関係数：

Rでの実行：

> library(vcd)
> mtx2 <- matrix(c(13,6,4,6,8,7,5,13,21), nrow=3, byrow=TRUE)
> vcd::assocstats(mtx2)
                    X^2 df  P(> X^2)
Likelihood Ratio 15.286  4 0.0041429
Pearson          15.244  4 0.0042217
Phi-Coefficient   : NA 
Contingency Coeff.: 0.394 
Cramer's V        : 0.303 

SASでの実行：

data ads;
input FACTOR OUTCOME CNT @@;
datalines;
1 0 13 1 1 6 1 2 4 2 0 6 2 1 8 2 2 7 3 0 5 3 1 13 3 2 21
;
run;
proc freq data=ads;
  table FACTOR * OUTCOME / chisq nocol nopercent;
  weight CNT / zeros;
  output out=Outds chisq;
run;

（※SASは２×２以上もファイ係数を計算するみたい）
  

プログラムコード

---

■ Rのコード

library(vcd)
vcd::assocstats(mtx1)

■ SASのコード

proc freq data=[InputDS];
 table VAR1 * VAR2 / chisq nocol nopercent;
 weight CNT / zeros;
 output out=[OutputDS] chisq;
run;

※カイ二乗検定で一緒に出力してくれる。

■ Pythonのコード

整備中

参考

---

統計学（出版：東京図書）, 日本統計学会編

【統計】相関係数（ピアソン、スピアマン、ケンドール）

相関係数について。

【目次】

計算式等

---

2変量を x, y とし、x の順位を z、y の順位を w として考える。タイ（同一順位）は平均順位を用いる。

ピアソンの積率相関係数（Pearson product-moment correlation coefficient）

スピアマンの順位相関係数（Spearman's rank correlation coefficient）

ケンドールの順位相関係数（Kendall rank correlation coefficient）

　※ただし、i を基準として、i＜ j の組合せのみ。

散布図を描いて考えると、次を数えている。
　A=プロット {} を基準として、右上or左下にあるプロット数の総和。
　B=プロット {} を基準として、左上or右下にあるプロット数の総和。
　C=プロット {} を基準として、xが同値でない数の総和。
　D=プロット {} を基準として、yが同値でない数の総和。

計算例

---

次の２変量の相関係数を見てみる。簡単のため、データ数は少なくしている。

　X={1, 2, 4, 7, 9, 10}, Y={1, 1, 6, 4, 10, 10}

グラフにすると次のとおり。 

Excelでの計算は以下。

相関係数

ピアソンの積率相関係数

Xの平均=5.5, Y の平均=5.335のため次の計算。

スピアマンの順位相関係数

X, Yについて順位を付けたものをZ, Wとする。
Zの平均=3.5, Wの平均=3.5のため次の計算。

ケンドールの順位相関係数

A～Dの計算は、X, Yの順序で整列した {1,1}, {2,1}, {4,6}, {7,4}, {9,10}, {10,10} について、
個々のペアを基準として、自分より後ろのデータとの関係を調べている。

● AとBの計算例：

１番目のペア {1, 1} を基準にすると、次のようにA該当４個（０より大きいもの）、B該当０個（０より小さいもの）。
　{1, 1} vs. {2, 1}=(1-2)(1-1)=0
　{1, 1} vs. {4, 6}=(1-4)(1-6)=15
　{1, 1} vs. {7, 4}=(1-7)(1-4)=18
　{1, 1} vs. {9, 10}=(1-9)(1-10)=72
　{1, 1} vs. {10, 10}=(1-10)(1-10)=81

また、３番目のペア {4, 6} を基準にすると、A該当２個、B該当１個。
　{4, 6} vs. {7, 4}=(4-7)(6-4)=-6
　{4, 6} vs. {9, 10}=(4-9)(6-10)=20
　{4, 6} vs. {10, 10}=(4-10)(6-10)=24

このような手順で全ペアの該当件数を算出して総和する。

● CとDの計算：
Yの１番目 {1} を基準とすると、次のようにD該当４個（同値でないもの）。
　{1} vs. {1}=同値
　{1} vs. {6}=同値ではない
　{1} vs. {4}=同値ではない
　{1} vs. {10}=同値ではない
　{1} vs. {10}=同値ではない

また、Yの５番目 {10} を基準とすると、次のようにD該当は０個。
　{10} vs. {10}=同値

このような手順で全ての値での該当件数を算出して総和する。

※全ペアの結果は、貼付した Excel Q:AH列 を参照のこと。

Rでの実行：

> ADS1 <- data.frame(X=c(1,2,4,7,9,10), Y=c(1,1,6,4,10,10))
> ADS1$Z <- rank(ADS1$X)
> ADS1$W <- rank(ADS1$Y)
> ggplot(ADS1) + geom_point(aes(X, Y), size=5, color="blue")
> cor(ADS1$X,ADS1$Y,method="pearson")
[1] 0.906666
> cor(ADS1$X,ADS1$Y,method="spearman")
[1] 0.9121593
> cor(ADS1$Z,ADS1$W,method="pearson") #--順位をpearsonで計算しても同じ。
[1] 0.9121593
> cor(ADS1$X,ADS1$Y,method="kendall")
[1] 0.7877264

なお、順位に変換してからピアソンの相関係数を算出すれば、スピアマンの順位相関係数が得られる。

SASでの実行：

data ads;
input x y @@;
cards;
1 1 2 1 4 6 7 4 9 10 10 10
;
run;
proc corr data=ads pearson spearman kendall;
  var x y;
run;

プログラムコード

---

■ Rのコード

cor(ADS$X, ADS$Y, method="pearson")  #-- ピアソンの積率相関係数
cor(ADS$X, ADS$Y, method="spearman") #-- スピアマンの順位相関係数
cor(ADS$X, ADS$Y, method="kendall")  #-- ケンドールの順位相関係数

■ SASのコード

proc corr data=ads pearson spearman kendall;
  var x y;
run;

■ Pythonのコード

整備中

ピアソンの相関係数と順位相関係数

---

ピアソンの相関係数は、線形の関係性を示す。
一方、スピアマンやケンドールの順位相関係数は順位を扱うため、例えば次の曲線の場合、ピアソンの相関係数＝0.98 に対して、スピアマンやケンドールの順位相関係数は１になる。  

> ADS2 <- data.frame(X=c(1,2,3,4,5,6,7,8,9,10)
+                    ,Y=c(2,2.1,2.5,3,4,5,6,7.5,7.9,8))
> ggplot(ADS2) + geom_point(aes(X, Y), size=5, color="blue")
> cor(ADS2$X,ADS2$Y,method="pearson")
[1] 0.9807044
> cor(ADS2$X,ADS2$Y,method="spearman")
[1] 1
> cor(ADS2$X,ADS2$Y,method="kendall")
[1] 1

参考

---

統計学（出版：東京図書）, 日本統計学会編

【統計】統計関連記事のサイトマップ

統計関係の記事いくつか書いているので、サイトマップ作りました。

差の評価

---

対応有無	目的変数	群数	検定	記事
対応なし	連続値	２群	t検定（Student、Welch）	記事あり
		２群以上	一元配置分散分析	記事あり
			二元配置分散分析	記事あり
			共分散分析	記事あり
	連続値 or順序変数	２群	Wilcoxonの順位和検定 マンホイットニーのU検定 ①正規近似、T近似 ②正確確率	①記事あり ②記事あり
		２群以上	Kruskal-Wallis test	記事あり
対応あり	連続値	２群	対応のあるt検定	記事あり
		２群以上	一元配置反復測定分散分析	記事あり
		２群以上	二元配置反復測定分散分析	記事あり
	連続値 or順序変数	2群	Wilcoxonの符号付き順位検定 ①正規近似、T近似 ②正確確率	①記事あり ②記事あり
		２群以上	フリードマン検定	記事あり

対応有無	目的変数	セル	検定	記事
対応なし	カテゴリ	n×m	Fisher's exact test	記事あり
			χ^2検定	記事あり
		k×n×m	マンテル・ヘンツェルの検定（CMH検定）	記事あり
対応あり		n×m	マクネマー検定	記事あり

傾向性の評価

---

目的変数	検定	記事
連続変数 or順序変数	ヨンキー検定（Jonckheere-Terpstra test）	記事あり
割合	コクランアミテージ検定	記事あり

関係性の評価

---

目的変数	検定	記事
連続変数	ピアソンの相関係数	記事あり
連続変数 or順序変数	スピアマンの順位相関係数 ケンドールの順位相関係数
カテゴリ	ファイ係数 ピアソンの連関係数（一致係数） クラメールの連関係数（クラメールのV）	記事あり

多変量解析

---

解析手法	記事
単回帰分析	記事あり
重回帰分析	記事あり
ロジスティックス回帰（理論編）	記事あり
ロジスティックス回帰（モデル評価編：ROC曲線、AUC、ホスマーレメショウ検定等）	記事あり
Lasso回帰（L1正則化）、Ridge回帰（L2正則化）	記事あり 記事あり
一般化線形モデル（GLM）	記事あり
一般化線形混合モデル（GLMM）	記事あり
主成分分析	記事あり
因子分析（探索的因子分析・検証的因子分析）	記事なし

生存時間解析

---

解析手法	記事
Kaplan-meier法	記事あり
ログランク検定、一般化Wilcoxon検定（Gehan's Wilcoxon）等	記事あり
コックス比例ハザードモデル	記事あり

 時系列解析

---

解析手法	記事
自己相関・自己共分散	記事あり
ARIMAモデル、SARIMAモデル、ARIMAXモデル（理論編）	記事あり
ARIMAモデル、SARIMAモデル、ARIMAXモデル（実装編）	記事あり
状態・空間モデル	記事なし
階層ベイズモデル	記事なし

あとがき

---

一先ず、書いてみたいと思った内容をまとめたが。。
すべて書くかは分からない。。。

【統計】クラスカル・ウォリス検定（Kruskal-Wallis test）

クラスカル・ウォリス検定（Kruskal-Wallis test）について。

【目次】

クラスカル・ウォリス検定（KW検定）は３標本以上を評価するノンパラメトリックな手法。
Wilcoxonの順位和検定・マンホイットニーのU検定（以下、Wilcoxonの順位和検定等）は２標本。
 

帰無仮説、対立仮設

---

• 帰無仮説 全ての標本の確率分布に差がない（ズレていない）。
• 対立仮設 何れかの標本の確率分布に差がある（ズレている）。

Wilcoxonの順位和検定等と同じく、確率分布の位置のズレを見る。正規分布に依存しないのが特徴。

計算式等

---

順位和

統計量の算出前に、先ず、比較したい全標本の観測値に全体順位（Rank）をつけて、標本ごとの合計（順位和）を算出する。観測値にタイ（同一順位）がある場合は、順位の平均値をつける。この方法はWilcoxonの順位和検定等と同じ。

H統計量

H統計量は近似的に 分布（）に従うため、 分布を使って検定を行う。

また、タイ（同一順位）の補正を行う場合、上で求めたH統計量にタイの補正値（D）を除算する。

Wilcoxonの順位和検定等と同じくタイ（同一順位）の補正式第２項の t が同一値の個数を示す。
例えば、{10,10,11,12,12,12} のデータがあるとき、10が２つ、11が１つ、12が３つになるため、それぞれ となり、 の計算で  になる。タイがない数値は解が０になり、タイにだけ働く。
なお、タイがまったくない場合は第２項の解全体が０になり、D=1-0=1になる。 で等価。
  

計算例

---

今回は、架空の４標本に違いがあるか評価する。

　A {10,10,11,12,12,12}
　B {12,13,14,17,19}
　C {12,14,15,19,20}
　D {16,17,18,20}

Excelでの計算：

Kruskal-Wallis test

Excelの簡単な説明。
・A列：標本のグループ名。
・B列：観測値。小さい順にならべている。
・C列：同値の数を上から数ている（セルC4：=IF(B3<>B4,1,D3+1)）。
・D列：同値の最終行のみ表示している（セルD4：=IF(B4=B5,"",C4)）。
・E列：分散の補正項用（セルE4：=IF(D4<>"",D4^3-D4,"")）
・G列：標本Aの順位（セルG4：=IF($A4=G$3, RANK.AVG($B4,$B:$B,1), "")）
・H列：標本Bの順位（セルH4：=IF($A4=H$3, RANK.AVG($B4,$B:$B,1), "")）
・I列 ：標本Cの順位（セルI4 ：=IF($A4=I$3, RANK.AVG($B4,$B:$B,1), "")）
・J列：標本Dの順位（セルJ4：=IF($A4=J$3, RANK.AVG($B4,$B:$B,1), "")）

H統計量：

順位和は だったため、 はそれぞれ になる（Excel L3:P7）。
全体数はN＝20のため、公式通り、H統計量は  となる（Excel L9:M15）。

 
タイの補正：

同一値 t の計算（）は 150 になる（Excel D:E, P12）。
（今回は 12 が５つあり、 と大きな値がある。）
公式通り、 となり、このDで除算して が得られる（Excel P13:P15）。

p値：

計算式等で述べたとおり、H統計量は 分布（）に従うため、次のようになる。


今回の架空データでは、標本間に差がある（p<0.01）。（タイ補正有無問わず）

Rでの実行： 

> ads <- data.frame(
+   AVAL    = c(10,10,11,12,12,12,12,12,13,14,14,15,16,17,17,18,19,19,20,20)
+   ,TRT01P = c("A","A","A","A","B","A","A","C","B","B","C","C","D","B","D","D","C","B","C","D"))
> ads$TRT01PF <- factor(ads$TRT01P)
> kruskal_test(AVAL ~ TRT01PF, data=ads, method="exact")

	Asymptotic Kruskal-Wallis Test

data:  AVAL by TRT01PF (A, B, C, D)
chi-squared = 11.722, df = 3, p-value = 0.0084

> kruskal.test(x=ads$AVAL, g=ads$TRT01PF)

	Kruskal-Wallis rank sum test

data:  ads$AVAL and ads$TRT01PF
Kruskal-Wallis chi-squared = 11.722, df = 3, p-value = 0.0084 

デフォルトで使える kruskal.test、coinパッケージのkruskal_testの２つ関数がありますが、どちらもタイ補正ありの結果を得る。
 

SASでの実行：

タイ補正ありの結果が得られる。

data ads;
  do AVAL=10,10,11,12,12,12; TRT01PN=1; output; end;
  do AVAL=12,13,14,17,19; TRT01PN=2; output; end;
  do AVAL=12,14,15,19,20; TRT01PN=3; output; end;
  do AVAL=16,17,18,20; TRT01PN=4; output; end;
run;
proc sort data=ads: by AVAL TRT01PN; run;
proc npar1way data=ads wilcoxon;
  class TRT01PN;
  var   AVAL;
  output out=OutputDS wilcoxon;
run;

プログラムコード

---

■ Rのコード

#-- coinパッケージ
library(coin)
kruskal_test(AVAL ~ Group, data=ADS, method="exact")

#-- デフォルトのstatsパッケージ
kruskal.test(x=ADS$AVAL, g=ADS$Group)

■ SASのコード

proc npar1way data=[InputDS] wilcoxon;
  class Group;
  var   AVAL;
  output out=[OutputDS] wilcoxon; /*_KW_,P_KWを取得。*/
run;

■ Pythonのコード

整備中

2標本でもKW検定

---

２標本のデータについて、Wilcoxonの順位和検定とKW検定を実行すると、どちらも同じ p値が得られる。

> ads <- data.frame(
+   TRT01P <- c("A","A","A","A","A","A","A","A","B","B","B","A","A","B","B","A","B","B","B","B")
+   ,AVAL  <- c(4,9,10,11,12,13,13,15,16,16,17,18,18,19,19,20,22,22,23,25)
+ )
> ads$TRT01PF <- factor(ads$TRT01P)
> wilcox_test(AVAL ~ TRT01PF, data=ads, method="exact")

	Asymptotic Wilcoxon-Mann-Whitney Test

data:  AVAL by TRT01PF (A, B)
Z = -2.9305, p-value = 0.003384
alternative hypothesis: true mu is not equal to 0

> kruskal_test(AVAL ~ TRT01PF, data=ads)

	Asymptotic Kruskal-Wallis Test

data:  AVAL by TRT01PF (A, B)
chi-squared = 8.5878, df = 1, p-value = 0.003384  

参考

---

https://www.dataanalytics.org.uk/adjustment-for-tied-ranks-in-the-kruskal-wallis-test/

https://www.lexjansen.com/wuss/2018/26_Final_Paper_PDF.pdf

---

★サイトマップ

cochineal19.hatenablog.com